А б в

Накопителем энергии - емкостью

Расчет переходных процессов в цепях с одним

Электромагнитные процессы при переходном процессе в таких цепях обусловлены запасом электрической энергии в емкости С и рассеиванием этой энергии в виде тепла на активных сопротивлениях цепи. При составлении дифференциального уравнения следует в качестве неизвестной функции выбрать напряжение u C на емкости. Следует отметить, что при расчете установившихся режимов, т. е. при определении начальных условий и принужденной составляющей, сопротивление емкости в цепях постоянного тока равно бесконечности.

Пример 6.2. Включение последовательной цепи R,C на постоянное напряжение.

Цепь (рис. 6.3, а ), состоящая из последовательно соединенных сопротивления R = 1000 Ом и емкости С = 200 мкФ, в некоторый момент времени подключается к постоянному напряжению U= 60 В. Требуется определить ток и напряжение емкости в переходном процессе и построить графики u C (t ), i (t ).

R i R i, A u, B

U C U C t = 0.02,c

0 t 2t 3t t , с

Решение. 1. Определяем начальные условия. Начальное условие u C (-0) = 0, так как цепь до коммутации была отключена (полагаем достаточно длительное время).

2. Изображаем электрическую цепь после коммутации (рис. 6.3, б ), указываем направления тока и напряжений и для нее составляем уравнение по второму закону Кирхгофа

или .

3. Преобразуем уравнение п.2 в дифференциальное. Для этого, подставив вместо тока i известное уравнение , получим:

4. Решение уравнения (искомое напряжение на емкости) ищем в виде:

.

5. Определяем . Так как в цепи постоянного тока в установившемся режиме сопротивление емкости равно бесконечности (при этом ), то все напряжение будет приложено к емкости. Поэтому

u C пр =U= 60 В.

6. Составляем однородное дифференциальное уравнение

решением которого будет функция

7. Составляем характеристическое уравнение RC l + 1= 0, корень которого равен

Постоянная времени

8. Запишем решение .

9. Согласно второму закону коммутации и начальным условиям

10. Определим постоянную интегрирования А путем подстановки t =0 в уравнение п.8

Напряжение на емкости в переходном процессе

11. Ток в цепи можно определить по уравнению

или по уравнению п. 2

Графики u C (t ) и i (t ) представлены на рис. 6.3, в .

Мгновенные значения токов и напряжения, определяющие энергетическое состояние электрической цепи, называются в данном методе переменными, а сам метод назван методом переменных состояния.

Этот метод основан на составлении системы дифференциальных уравнений и, как правило, численном их решении с помощью ЭВМ.

В качестве неизвестных здесь следует принимать переменные, которые не имеют разрывов, т.е. за время не должно быть скачкообразного изменения этих величин. Такими переменными, следовательно, должны быть ток i и потокосцепление в индуктивности, напряжение и заряд на емкости. В противном случае при численном решении производных в точках, где имеется разрыв, возникает бесконечно большая величина, что недопустимо.

Существуют различные численные методы расчета дифференциальных уравнений. Это методы Эйлера, Рунге-Кутта и другие, которые отличаются друг от друга точностью расчета, объемом и временем вычислений. При этом, чем больше точность вычислений, тем больше требуется времени для решения.

1. Определить начальные условия.

2. Составить систему дифференциальных уравнений.

3. Все переменные в уравнениях п.2 выразить через токи или потокосцепления в индуктивностях и напряжения или заряды на емкостях.

4. Все уравнения п.3 свести к нормальной форме Коши.

Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости или (и) переходную функцию по напряжению , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как , а вторую - как t.

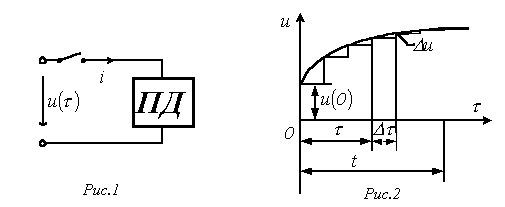
Пусть в момент времени к цепи с нулевыми начальными условиями (пассивному двухполюснику ПД на рис. 1) подключается источник с напряжением произвольной формы. Для нахождения тока в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.

В момент времени t составляющая общего тока, определяемая начальным скачком напряжения , равна .

В момент времени имеет место скачок напряжения , который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока .

Полный ток в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом , т.е.

Заменяя конечный интервал приращения времени на бесконечно малый, т.е. переходя от суммы к интегралу, запишем

.

(1)

Соотношение (1) называется интегралом Дюамеля.

Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости будет входить переходная функция по напряжению.

Последовательность расчета с использованием
интеграла Дюамеля

В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.

Исходные данные для расчета: , , .

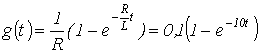
Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.

Метод переменных состояния

Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.

Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.

Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.

К уравнениям состояния выдвигаются два основных требования:

Независимость уравнений;

Возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.

Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.

Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.

При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные и с самими переменными и и источниками внешних воздействий – ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих искомые величины с переменными состояния и источниками внешних воздействий.

Таким образом, полная система уравнений в матричной форме записи имеет вид

;

(2)

.

(3)

Здесь и - столбцовые матрицы соответственно переменных состояния и их первых производных по времени; - матрица-столбец источников внешних воздействий; - столбцовая матрица выходных (искомых) величин; - квадратная размерностью n x n (где n – число переменных состояния) матрица параметров, называемая матрицей Якоби; - прямоугольная матрица связи между источниками и переменными состояния (количество строк равно n, а столбцов – числу источников m); - прямоугольная матрица связи переменных состояния с искомыми величинами (количество строк равно числу искомых величин к, а столбцов – n); - прямоугольная размерностью к x m матрица связи входа с выходом.

Начальные условия для уравнения (2) задаются вектором начальных значений (0).

В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи и .

По законам Кирхгофа для данной цепи запишем

;

(5)

Матричное уравнение вида (3) вытекает из соотношений (4) и (6):

Вектор начальных значений (0)= .

Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.

Методика составления уравнений состояния

Эта методика включает в себя следующие основные этапы:

1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.

2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).

3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.

Таблица 1 . Таблица соединений

Процедура заполнения таблицы заключается в поочередном мысленном замыкании ветвей дерева с помощью ветвей связи до получения контура с последующим обходом последнего согласно ориентации соответствующей ветви связи. Со знаком «+» записываются ветви графа, ориентация которых совпадает с направлением обхода контура, и со знаком «-» ветви, имеющие противоположную ориентацию.

Осуществляется расписывание таблицы по столбцам и по строкам. В первом случае получаются уравнения по первому закону Кирхгофа, во втором – по второму.

В рассматриваемом случае (равенство тривиально)

,

откуда в соответствии с нумерацией токов в исходной цепи

.

При расписывании таблицы соединений по строкам напряжения на пассивных элементах необходимо брать со знаками, противоположными табличным:

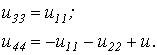(7)

Эти уравнения совпадают соответственно с соотношениями (6) и (5).

Из (7) непосредственно вытекает

.

Таким образом, формализованным способом получены уравнения, аналогичные составленным выше с использованием законов Кирхгофа.

Литература

1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. радиотехн. спец. вузов. 3-е изд., перераб. и доп. –М.: Высш. шк., 1990. –400с.

Контрольные вопросы и задачи

А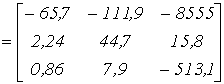
В

Основы > Теоретические основы электротехники

Метод переменных состояния
Уравнениями состояния можно назвать любую систему уравнений, определяющих режим цепи. В более узком смысле - это система дифференциальных уравнений первого порядка, разрешенная относительно производных.
Методом переменных состояния назовем анализ цепи, основанный на решении уравнений состояния (первого порядка), записанных в форме Коши. Таким образом, метод переменных состояния - один из методов расчета прежде всего переходных процессов. Далее предполагается, что цепь имеет только независимые источники и не содержит индуктивных сечений и емкостных контуров. В противном случае составление уравнений становится намного сложнее.
Для линейной цепи с постоянными сосредоточенными параметрами ток каждой ветви, напряжение между выбранными выводами, заряд на обкладках конденсатора и т. д. всегда можно найти как решение составленного для этого тока, напряжения, заряда и т. д. дифференциального уравнения (например, исключением других токов и напряжений из системы уравнений Кирхгофа):

Введением переменных это уравнение сводится к эквивалентной системе дифференциальных уравнений первого порядка:

Здесь переменными, которые называются переменными состояния , служат переменная х и ее производные.
Как известно, переходный процесс в любой цепи, кроме ее параметров (значений r , L, С, М) и действующих источников [ e(t) и J(t)], определяется независимыми начальными (t = 0) условиями - токами в индуктивных элементах и напряжениями на емкостных элементах , которые должны быть известны или рассчитаны. Через них выражаются искомые величины во время переходного процесса. Они же определяют энергетическое состояние цепи. Поэтому в качестве переменных состояния целесообразно выбирать токи и напряжения . Действующие источники можно назвать входными величинами , искомые величины - выходными . Для цепи с n независимыми токами и напряжениями должны быть заданы еще n независимых начальных условий.

Сокращенно дифференциальные уравнения состояния запишем в матричной форме так:

или короче

где X матрица-столбец (размера n x 1) переменных состояния (вектор переменных состояния); F - матрица-столбец (размера m x 1) ЭДС и токов источников (внешних возмущений); А - квадратная матрица порядка n (основная); В - матрица размера п х m (матрица связи). Элементы этих матриц определяются топологией и параметрами цепи.
Для выходных величин (если определяются не токи в индуктивных и напряжения на емкостных элементах) в матричной форме система алгебраических уравнений имеет вид

или короче

где W - матрица-столбец (размера l x 1 ); M - матрица связи (размера l x n ); N - матрица связи (размера l x m ).
Элементы матриц зависят от топологии и параметров цепи. Для уравнений состояния разработаны и машинные алгоритмы формирования на основе топологии и значений параметров.
Уравнения в матричной форме (14.91) можно составить, например, с применением метода наложения. Для получения зависимостей между производными переменных состояния, т. е. и переменными состояния , а также ЭДС и токами источников, действующими в цепи, будем считать, что переменные состояния заданы. Рассматриваемую цепь, например на рис. 14.41, а, заменим после коммутации эквивалентной (рис. 14.41,6), у которой каждый заданный ток представлен источником тока , а каждое заданное напряжение - источником напряжения (ЭДС) . Применив метод наложения (положительные направления выбраны), запишем напряжения и токи (сначала учитываем действие источников затем и далее источников, действующих в цепи):

Так как , то

Конечно, уравнения (14.93) можно получить и из уравнений Кирхгофа исключением токов и напряжений ре-зистивных элементов. Однако совместное решение уравнений Кирхгофа с увеличением числа ветвей цепи становится все более громоздким.
Уравнения состояния можно формировать и сразу в матричной форме.
Если источников тока и ЭДС нет, т. е. F = 0, то уравнения (14.91) упрощаются

и характеризуют свободные процессы в цепи. Решение запишем в виде

где X (0) - матрица-столбец начальных значений переменных состояния; - матричная экспоненциальная функция.
Подставив (14.94) в (14.91в), убедимся, что получается тождество.
При решение уравнения (14.91) представим в виде

где Ф(t ) - некоторая матричная функция цепи. После дифференцирования (14.95) получим

Сравним (14.96) с (14.91а)

и, умножив на , после интегрирования найдем, что

где q - переменная интегрирования, или



Подставим это выражение в (14.95):



В частности, при t = 0 имеем
Следовательно, решение для переменных состояния записывается в виде


(реакция цепи равна сумме реакций при нулевом входе и при нулевом начальном состоянии).
Это решение можно получить и применив операторный метод расчета переходных процессов, рассматриваемый в разделе .
Выходные величины можно найти по (14.92).
Если состояние цепи задано не при t = 0, а при , то в (14.97) первое слагаемое записывается так: , а нижний предел интеграла не 0, а t .
Главная трудность расчета заключается в вычислении матричной экспоненциальной функции. Один из путей такой: сначала находим собственные значения l матрицы А, т. е. корни уравнения

где 1 - единичная матрица порядка n , которые определяются из уравнения

где - элементы матрицы А.
Собственные значения совпадают с корнями характеристического уравнения цепи.
Матричная экспонента, аргумент которой - матрица А t , имеющая порядок n , представима конечным числом n слагаемых. Если собственные значения различны, то

Где - функции времени; и т. д.
Далее для определения составляем алгебраическую систему n уравнений

Наконец, определив из (14.100), по (14.99) находим и затем X (t) по (14.97).

Пример 14.6. Определить ток в цепи на рис. 14.42 после коммутации при .

Решение. Выбираем положительные направления токов в индуктивных элементах, т. е. переменных состояния, и тока . Независимые начальные условия: . Дифференциальные уравнения цепи

Исключив ток , получим уравнения относительно производных переменных состояния:

т. е. согласно (14.91)

и матрица-столбец начальных значений

Вычислим собственные значения; по (14.98)

откуда . Если приравнять нулю главный определитель уравнений с переменными состояния, то получим те же значения .
Находим коэффициенты ак по (14.100), т. е. из системы уравнений

Значения тока вычисленные в моменты секунд для интервала времени 0 - 0,1 с, в конце которого ток отличается от установившегося менее чем на 1,5%, приведены в табл. 14.1. При вычислениях цифры записывались с 8 разрядами, а во всех приведенных в примере формулах и в табл. 14.1 указаны с округлением.

Таблица 14.1

	0,005	0,010	0,015	0,020	0,025	0,030	0,035	0,040	0,045	0,050
	1,079	1,213	1,343	1,455	1,550	1,628	1,692	1,746	1,790	1,827
	0,055	0,060	0,065	0,070	0,075	0,080	0,085	0,090	0,095	0,100
, то для n - q разных корней составляется система (14.100), а для q кратных уравнения получаются после вычисления первых q - 1 производных по от обеих частей уравнения с корнем , т. е. Если в цепи действует только один источник ЭДС (или тока), представляющий единичный скачок 1( t ), т. е. F(t )=1(t ), и начальные условия нулевые, то решение (14.97) запишется в виде Для выходных величин по (14.92а) получим Это будут переходные функции цепи h(t). Импульсные переходные функции k (t ) определяются по (14.84) или (14.85). Более общим путем вычисления матричной экспоненциальной функции служит ее представление бесконечным рядом но ряд при больших t медленно сходится. При ограничении конечным числом слагаемых вычисление сводится к умножению и суммированию матриц. Такие операции есть в математическом обеспечении ЭВМ. Известен метод вычисления матричной экспоненциальной функции, основанный на критерии Сильверста. Уравнения состояния цепей, порядок которых больше двух-трех, проще решаются не аналитическими, а численными методами, дающими возможность автоматизировать расчет в случае применения ЭВМ.

Расчет переходных процессов в линейных электрических цепях методом переменных состояния

Это наиболее универсальный метод расчета цепей как них, так и нелинейных. Метод используется для расчета цепей высокого порядка, когда применение других методов расчета нецелесообразно или практически невозможно. Метод переменных состояния основан на решении уравнений состояния (первого порядка)записанных в форме Коши. Для решения системы уравнений первого порядка разработаны численные методы, позволяющие автоматизировать расчет переходных процессов с ЭВМ. Таким образом, метод переменных состояния - один из расчета переходных процессов, ориентированный прежде всего на применение ЭВМ.

Для линейной цепи с постоянными сосредоточенными параметрами ток каждой ветви, напряжение между выводами, заряд на обкладках, конденсатора и т. д. можно найти как решение дифференциального уравнения, составленного для этого тока, напряжения, заряда и т.д., исключением других токов и напряжений из системы уравнений Кирхгофа:

Введением переменных

уравнение (1.1) сводится к эквивалентной системе дифференциальных уравнений первого порядка:

(1.2)

Здесь переменными, которые называются переменными состояния, служит переменная X и ее производные. При этом предполагается, что цепь имеет только независимые источники и не содержит индуктивных сечений и емкостных контуров. В противном случае составление уравнений становится намного сложнее

1. Формирование уравнений переменных состояния

Энергетическое состояние цепи, а следовательно, и переходный процесс в любой цепи определяется энергией магнитного поля, запасенной в индуктивностях, и энергией электрического поля, запасенной в емкостях. Запасы энергии в реактивных элементах определяют токи в индуктивностях и напряжения емкостей, т.е. они определяют энергетическое состояние цепи и поэтому принимаются в качестве независимых переменных состояния.

Любая система уравнений, определяющая состояние цепи, называется уравнениями состояния. Токи в индуктивных элементахи напряжения на емкостных элементах
представляют независимыеначальные условия
цепи и должны быть известны или рассчитаны. Через них выражаются искомые величины во времяпереходного процесса.

Действующие источники энергии принято называть входными величинами
,а искомые величины (токи и напряжения) - выходными величинами
.

Для цепи с n независимыми токами и напряжениями
должны быть заданы еще n независимых начальных условий. Для операций с большим числом переменных используют методы матричного исчисления.

Сокращенно дифференциальные уравнения состояния, описывающие цепь по законам Кирхгофа, записываются в матричной форме:

, (1.3)

где X - вектор-столбец (размером n х 1) произвольных переменных состояния; V - вектор-столбец (размером m х 1) внешних воздействий (ЭДС и токов источников); А - квадратная матрица порядка n (основная); В - матрица связи между входами цепи и переменными состояния (размера n х m). Элементы этих матриц определяются топологией и параметрами цепи
,m - число входов, n - число переменных состояния.

Для выходных величин (если определяются не токи в индуктивностях и напряжения на емкостных элементах) необходимо добавить еще уравнение в матричной форме:

(1.4)

где Y - вектор - столбец искомых токов и напряжений на выходе (размерен 1 х 1), 1 - число выходов; С - матрица связи переменных состояния с выходами цепи (п х 1); D - матрица непосредственной связи входов и выходов цепи (размером 1 х m). Элементы матриц зависят от топологии и значений параметров цепи
.

Систему матричных уравнений

;
(1.5)

можно представить в виде структурной схемы (рис.1.3).

1.1. Составление уравнений состояния цепи

методом наложения

Пусть дана схема цепи после коммутации

Будем считать, что переменные состояния заданы. Рассматриваемую цепь (рис.2) заменим после коммутации эквивалентной (рис.3), у которой заданный ток представлен источником тока,заданное напряжение
источником напряжения
.

Применив метод наложения (положительные направления выбраны), запишем напряжения
и токи
(сначала учитываемдействие источника затем
и далее источников, действующих в цепи).

От действия :

;
;

от действия
:

;
;

от действия е:

;
,

а полный ток
и напряжение .

(1.6)

Учитывая, что
и
получим

т.е в матричном виде уравнение (1.7) запишемся

(1.8)

1.2. Составление уравнений состояния цепи с помощью

законов Кирхгофа

Уравнения (1.7) можно получить и из уравнений Кирхгофа исключением токов и напряжений резистивных элементов. По законам Кирхгофа уравнения для цепи (см.рис. 2) запишем в виде

(1.9)

Разрешим первое уравнение системы относительно , атретье, учитывая, что
, относительно. Тогда

(1.10)

Переменные
иявляются переменными состояния длярассматриваемой цепи. В правой части системы (1.10) присутствует переменная , не являющаяся независимой переменной состояния. Для ее исключения перепишем второе уравнение системы (1.9) в виде

(1.11)

и подставим сюда
.

Полученное из (1.11) значение тока

(1.12)

подставим в систему (1.10).

Получим систему уравнений в переменных состояния
для исследуемой цепи

(1.13)

где X, X, V, А, В соответствуют системе уравнений (1.7).

Пусть в рассматриваемом примере требуется определить токи и . Следовательно и будут выходными величинами цепии их необходимо представить в виде
,
.Ток уже определен в требуемом виде (1.12), а ток
.Тогда вторая система уравнений в переменных состояния
примет вид

(1.14)

В матричной форме система уравнений (1.14) запишется в виде

(1.15)

В частном случае, если выходными переменными является переменные состояния
то матрица С принимает вид диагональной матрицы, а элементы матрицы D равны нулю.

Уравнения состояния решаются на компьютерах численными методами.

В. Н. Непопалов

Метод переменных состояния

Учебное пособие

Челябинск 2003

УДК 621.3.011(075.8)

Непопалов В. Н. Метод переменных состояния: Учебное пособие. – Нижневартовск, Изд. 2003.– 26 с.

Рассматривается метод переменных состояния расчета переходных процессов в линейных электрических цепях. Учебное пособиепредназначено в помощь студентам при самостоятельной работе по курсу «Дополнительные главы электротехники».

1. Нормальная форма уравнений состояния 4

2. Получение нормальной формы уравнений состояния 5

3. Примеры получения нормальной формы уравнений состояния 6

4. Решение уравнений состояния классическим методом 9

5. Использование элементов теории матриц для решения уравнений состояния 15

6. Применение к расчету переходных процессов 22

7. Контрольные вопросы 24

Метод переменных состояния

Переменными состояния будем называть определенный в момент времени t 0 набор функций (напряжений, потокосцеплений, токов или зарядов), значений которого вместе с заданными для t  t 0 входными воздействиями, достаточно для однозначного определения выходных функций для любого момента времени t  t 0 .

В качестве переменных состояния электрической цепи можно выбрать некоторый набор напряжений, зарядов, токов или потокосцеплений, определенных строго для момента времени , т. е. в момент непосредственно после коммутации. Это обстоятельство ограничивает возможность выбора переменных состояния напряжениями или зарядами на емкостях и токами или потокосцеплениями в индуктивностях, так как значения этих величин не изменяются в момент коммутации t  0:

,,,.

Число величин, определяющих количество переменных состояния, равно числу независимых физических начальных условий.

1. Нормальная форма уравнений состояния

Переменные состояния в момент времени t определяются матрицей-столбцом
, размерностью

С помощью переменных состояния математическая модель линейной электрической цепи, с независящими от времени параметрами, определяется совокупностью дифференциальных уравнений:

и алгебраических уравнений:

где X (t )– матрица-столбец переменных состояния размерностью
;

матрица-столбец производных переменных состояния;

F (t )– матрица-столбец заданных входных переменных или входных воздействий;

Y (t )– матрица-столбец выходных переменных;

А ,В ,С ,D – матрицы известных величин, причем,А – квадратная матрица порядкаn . Размерности матрицВ, С , D определяются условиями конкретной задачи.

Дифференциальные уравнения вида

будем называть нормальной формой уравнений состояния, а алгебраические уравнения вида

уравнениями выходных функций.

2. Получение нормальной формы уравнений состояния

Для получения нормальной формы уравнений состояния

1. Нарисовать направленный граф схемы электрической цепи. Составить для этого графа нормальное дерево. В нормальное дерево необходимо включить все ветви с емкостями и источниками э. д. с . Если этого недостаточно для получения дерева, добавить ветви с резисторами, если и этого недостаточно для получения дерева, добавить ветви с индуктивностями. Связями (хордами) графа должны быть ветви с индуктивностями, источниками тока и резистивными ветвями, не вошедшими в дерево графа.

2. Для каждой ветви дерева определить сечение, в которое входит только одна ветвь дерева и некоторый набор связей графа (хорд). Число независимых сечений равно числу ветвей дерева: b t  q – 1, где –q число узлов. Записать уравнения Кирхгофа для токов каждого главного сечения и выразить токи ветвей дерева через токи ветвей хорд. Основными из уравнений являются те, в которые входят токи емкостей (если они есть).

3. Для каждой связи определить контур, в который входит только одна связь и некоторый набор ветвей дерева. Число независимых контуров равно числу связей: b l  b – q+ 1, гдеb – число ветвей графа. Записать уравнения по второму закону Кирхгофа для каждого контура и выразить напряжения на индуктивностях (если они есть) через напряжения на других элементах. Если связями является ветви с источниками тока, то при составлении уравнений состояния уравнения по второму закону Кирхгофа для этих контуров не записываются. Основными являются те уравнения, в которые входят напряжения на индуктивностях.

4. С помощью оставшихся уравнений исключить из основных уравнений напряжения и токи резистивных ветвей. Выразить токов емкостей и напряжения на индуктивностях через напряжения на емкостях и токи в индуктивностях.

5. Подставить в основные уравнений уравнения элементов:

;
.

6. Преобразовать полученную систему в нормальную форму уравнений состояния.

7. Записать алгебраические уравнения выходных функций.